Cardanische Formel

Bemerkung

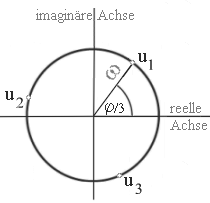
Um die Cardanische Formel richtig interpretieren zu können, sollte man wissen, dass zu jeder Zahl ungleich Null genau drei komplexe Kubikwurzeln existieren. Folglich hat u = (-b/2 + √b²/4 + a³/27)^1/3 im nichttrivialen Fall drei verschiedene Lösungen:

u1 = ω·exp(i·φ/3),
u2 = ω·exp( i·(φ+2)/3),
u3 = ω·exp( i·(φ+4)/3),

wobei ω die eindeutig bestimmte reelle Kubikwurzel aus der reellen Zahl |-b/2 + √b²/4 + a³/27| ist und φ den Winkel von -b/2 + √b²/4 + a³/27 bezeichnet.

Genauso ziehen wir aus  -b/2 - √b²/4 + a³/27 die drei Kubikwurzeln

v1 = θ·exp(i·Φ/3),
v2 = θ·exp( i·(Φ+2)/3),
v3 = θ·exp( i·(Φ+4)/3).

Für y = u + v gibt es daher neun Möglichkeiten; eine kubische Gleichung kann aber nicht mehr als drei Lösungen haben. Unsere Herleitung der Cardanischen Formel zeigt jedoch, dass es ein uj ∈ {u1, u2, u3} und ein vk ∈ {v1, v2, v3} gibt mit uj·vk = -a/3. Folglich löst auf jeden Fall uj + vk die kubische Gleichung (uj·vk = -a/3 ist hierfür notwendig und hinreichend).

Nun können wir die übrigen Lösungen leicht berechen und stellen hierzu die Menge {u1, u2, u3} in der Form {uj, uj·ε, uj·ε²} mit ε = exp( i·2/3) dar. Ebenso gilt: {v1, v2, v3} = {vk, vk·ε, vk·ε²}. Offensichtlich ist ε³ = 1 und daraus folgt: (uj·ε)·(vk·ε²) = (uj·ε²)·(vk·ε) = -a/3.  Damit haben wir folgende Lösungen:

y1 = uj + vk ,
y2 = uj·ε + vk·ε² ,
y3 = uj·ε² + vk·ε .

y1, y2, y3 sind zwar nicht stets paarweise verschieden, dennoch existieren niemals weitere Lösungen, weil nur die obigen drei Produkte die Zahl -a/3 liefern - es gilt nämlich: ε, ε² und ε⁴ ≠ 1.

Wir wenden die Cardanische Formel jetzt auf die Gleichung: y³ - 12y = 0 an (die man auch durch genaues Hinsehen lösen könnte). Hier ist u = (8i)^1/3, ω = 2 und φ = /2. Daraus folgt: u1 = 2·exp( i·/6), u2 = 2·exp( i·5/6), u3 = 2·exp( i·3/2). Ferner gilt: v1 = 2·exp( i·/2), v2 = 2·exp( i·7/6), v3 = 2·exp( i·11/6). Wegen u3·v1 = 4 = -a/3 lauten die Lösungen:

y1 = u3 + v1 = 0 ,
y2 = u3·ε + v1·ε² = 2·√3 ,
y3 = u3·ε² + v1·ε = -2·√3 .

In unserer Antwort bezeichnen wir den Fall D < 0 als Casus irreducibilis - was wir nun klären. Notwendig ist also a < 0, und u³ = -b/2 + √D ist die konjugiert-komplexe Zahl zu v³ = -b/2 - √D. Ferner gilt: ω = θ = √-a/3 sowie Φ = -φ. Das Produkt von u1 = ω·exp(i·φ/3) und v1 = ω·exp(-i·φ/3) ist gleich -a/3 und daraus folgt: y1 = u1 + v1 = 2ω·cos φ/3 ist eine Lösung der kubischen Gleichung. Ebenso kann man für y2 und y3 reelle Ausdrücke finden. Für D < 0 sind daher alle Lösungen in reeller Form darstellbar, obwohl sie zunächst als Summe von Kubikwurzeln nichtreeller Zahlen auftreten. Somit bleibt noch zu erörtern, wie die Bezeichnung „Casus irreducibilis” gerechtfertigt ist:
Es sei also D < 0 und y³+ay+b=0 die entsprechende kubische Gleichung über dem minimal gewählten reellen Zahlkörper K. Dann sind die Lösungen nicht durch reelle Radikale darstellbar, wenn die Gleichung irreduzibel über K ist. In diesem Fall lassen sich die Lösungen in reeller Form nur auf trigonometrische Weise exakt darstellen.

Beispiel: Der kleinste reelle Zahlkörper, der die Koeffizienten a = -3 und b = 1 der Gleichung y³ - 3y + 1 = 0 enthält, ist der Körper Q der rationalen Zahlen. Somit ist unser K = Q, und weil die Teiler von 1 keine Lösungen dieser normierten ganzzahligen Gleichung sind, gibt es weder ganzzahlige noch andere rationale Lösungen. Unsere kubische Gleichung ist daher irreduzibel über Q ist. Zudem ist die Diskriminante negativ, und folglich sind die Lösungen: y1 = 2ω·cos(φ/3) = 2·cos(2/9), y2 = 2·cos(8/9), y3 = 2·cos(14/9) nicht durch reelle Radikale darstellbar.

Ihren Namen hat die Cardanische Formel nach dem Mailänder Arzt und Mathematiker Hieronimo Cardano. Als ihre Entdecker gelten aber Scipione del Ferro (1465 - 1526) und Nicolo Tartaglia, die unabhängig voneinander das Lösungsverfahren entwickelten und es lange Zeit geheim hielten.



Bei einem mathematischen Wettstreit setzte Tartaglia seine Kenntnisse dann mit großem Erfolg ein, ohne die Formel preiszugeben. Das machte in Italien so viel Aufsehen, dass die gebildeten Leute regen Anteil an den Diskussionen über die Wunderformel nahmen. Cardano kam mit einer List schließlich hinter das Geheimnis und veröffentlichte das Verfahren gegen Tartaglias Willen.


Hinweis:

Oft wird behauptet, dass Tartaglia eigentlich Fontana hieß und nur wegen einer zeitweiligen Sprachstörung, die von einem Schwertstreich herrührte, Tartaglia (Stotterer) genannt wurde. Ein Mathematikhistoriker legte uns aber ausführlich dar, dass diese These falsch ist.