Startseite Mathematik-Online        Themenliste

Mathematik-Online

  rechtwinkliges Dreieck
Ein Dreieck nennt man rechtwinklig, wenn zwei Seiten (a und b) senkrecht aufeinander stoßen. Bereits vor mehr als 2.500 Jahren entdeckte der griechische Philosoph und Mathematiker Pythagoras, dass für alle rechtwinkligen Dreiecke die Beziehung: a²+b² = c² gilt. Der antike Beweis dieser Aussage ist ebenso elegant wie einfach und wurde seither auf vielfache Weise variiert. Allerdings sollte man nicht versuchen, hier einen vektoriellen Beweis zu führen, weil dabei stets ein Zirkelschluss herauskommt:

Satz des Pythagoras

Frage
Im Unterricht haben wir den Lehrsatz von Pythagoras mit dem Skalarprodukt s wie folgt bewiesen: c² = |v+w|² = s(v+w,v+w) = s(v,v) + s(w,w) + 2s(v,w). Weil v orthogonal zu w ist, gilt dann: 2s(v,w) = 0, daraus folgt: |v+w|² = s(v,v) + s(w,w) = |v|² + |w|² = a²+b².

Den Beweis finde ich einfach, aber warum ist s(v,v) = |v|² und s(w,w) = |w|² ?

Antwort

Man definiert |v|²:=s(v,v), weil das direkt den vektoriellen Pythagoras liefert. Das zeigen die obigen Schlussfolgerungen, mehr aber auch nicht. Mit der Gleichung: c² = |v+w|² wird nämlich der elementargeometrische Satz des Pythagoras als gültig vorausgesetzt. Die Argumentation aus Ihrem Unterricht ist also zirkulär.



Mathematik-Online, Satz des Pythagoras


Bemerkung

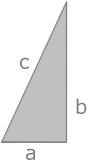
Die Standardnorm (Länge) eines Vektors u = (a,b) ∈ IR² ist durch die Zahl √s(u,u) = √a² + b²  definiert, wobei s hier das kanonische Skalarprodukt bezeichnet. Diese Vektornorm stimmt mit der elementargeometrischen Länge genau dann überein, wenn der klassische Lehrsatz des Pythagoras wahr ist. Daher ist es zirkulär, diesen Satz vektoriell beweisen zu wollen. Nun folgt eine korrekte Beweisführung:

Skizze zum Beweis des Satzes von Pythagoras
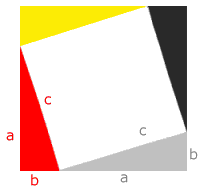
Die vier Dreiecke haben jeweils den Flächeninhalt ½·a·b. Ferner ist c·c der Flächeninhalt des inneren Quadrats. Der Inhalt des äußeren Quadrats beträgt (a+b)·(a+b). Andererseits setzt sich das äußere Quadrat aus den vier Dreiecken und dem inneren Quadrat zusammen. Somit gilt: (a+b)·(a+b) = 4·(½·a·b) + c·c. Daraus folgt: c² = a² + b².

Dagegen zeigt der vektorielle Beweis lediglich, dass in den entsprechend normierten Räumen für alle orthogonalen Vektoren v und w die Aussage: Norm²(v+w) = Norm²(v) + Norm²(w) gilt. Die euklidische Ebene kann man aber nur dann mit dem kanonisch normierten IR² identifizieren, wenn der elementargeometrische Beweis des Satzes von Pythagoras vorliegt. Hier schließt sich also der Kreis. Übrigens lassen sich Vektorräume auch derart normieren, dass man den Pythagoras daraus nicht mehr ableiten kann.
Themenliste Strahlensatz