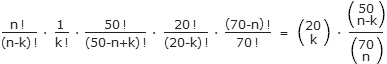Die Zahlenlotterie Keno ist inzwischen auch in Deutschland recht populär. Allerdings müssen die Keno-Spieler davon ausgehen, im Durchschnitt mehr als die Hälfte des Einsatzes zu verlieren. Bevor wir darauf näher eingehen, berechnen wir die Chancen für einen Keno-Volltreffer:

Bei der Keno-Lotterie kann man auch ohne einen Volltreffer gewinnen. Wir berechnen jetzt die Chance, mit n Kreuzen k Treffer zu erzielen:

Die ersten k der n angekreuzten Zahlen sind mit einer Wahrscheinlichkeit von 20! / (20-k)!  ×  (70-k)! / 70! Gewinnzahlen. Die verbleibenden n-k Zahlen sind mit der Wahrscheinlichkeit 50! / (50-n+k)! × (70-n)! / (70-k)! keine Gewinnzahlen. Zudem gibt es n!/(n-k)! Möglichkeiten, unter den n angekreuzten Zahlen k Treffer anzuordnen. Weil es aber bei der Auslosung nicht auf die Reihenfolge der Gewinnzahlen ankommt, muss man durch k! dividieren. Insgesamt beträgt somit die Chance für 0 ≤ k ≤ n Treffer bei n angekreuzten Zahlen: Mit Hilfe dieser hypergeometrischen Verteilung lässt sich berechnen, dass die Keno-Spieler im Durchschnitt nur knapp die Hälfte des Einsatzes wieder ausgezahlt bekommen, wenn sie auf 2, 4, 5, 6, 7, 8 oder 10 Zahlen tippen (siehe Tabelle). Bei 3 oder 9 angekreuzten Zahlen ist der Erwartungswert geringfügig höher.