Aus jeder natürlichen Zahl lassen sich unendlich viele Brüche konstruieren - dennoch kann man
alle Brüche mit Hilfe der natürlichen Zahlen paarweise verschieden nummerieren.
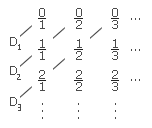Der Kunstgriff besteht darin, die nicht negativen
Brüche zweidimensional anzuordnen und diagonal
abzuzählen. In unserer Skizze liegt m/n auf der
Diagonale Dm+n an der n-ten Stelle und erhält somit die vorläufige Nummer
1 + 2 + ... + m + n
- 1 + n = ½·(n+m)·(n+m-1) + n. Mit der Zahl 2 multipliziert ergibt das für m/n die endgültige gerade Nummer (n+m)² + (n-m). Daher können wir -m/n die noch freie ungerade Nummer (n+m)² + (n-m) - 1 geben.
Unsere Nummerierung aller Brüche liefert (etwa durch Auswahl der jeweils kleinsten Nummer) eine Abzählung der rationalen Zahlen. Diese Methode bezeichnet man als „Cantors (Cantorsches) Diagonalverfahren”.
- 1 + n = ½·(n+m)·(n+m-1) + n. Mit der Zahl 2 multipliziert ergibt das für m/n die endgültige gerade Nummer (n+m)² + (n-m). Daher können wir -m/n die noch freie ungerade Nummer (n+m)² + (n-m) - 1 geben.
Unsere Nummerierung aller Brüche liefert (etwa durch Auswahl der jeweils kleinsten Nummer) eine Abzählung der rationalen Zahlen. Diese Methode bezeichnet man als „Cantors (Cantorsches) Diagonalverfahren”.
