
Fibonacci
ca. 1180 - 1250
Der italienische Mathematiker Leonardo von Pisa
(Fibonacci) hat sich folgende Frage gestellt:
Ein Paar neugeborener Kaninchen wirft nach zwei
Monaten ein neues Paar und in den folgenden Monaten jeweils ein weiteres Paar. Jedes
Paar vermehrt sich genauso. Wie viele Paare gibt es (Todesfälle ausgeschlossen) im Jahresverlauf ?
Von Monat zu Monat ist 1, 1, 2, 3, 5, 8, ... die Anzahl der Kaninchenpaare - jede Zahl > 1
ist die Summe der beiden vorangegangenen Zahlen, also gilt für alle n die Gleichung
a
n+2 =
a
n+1 + a
n. Um die n-te Fibonaccizahl
zu bestimmen, muss man aber nicht entsprechend oft addieren, sondern kann die
Formel von Jaques Binet (1786 - 1856) anwenden:
Fibonaccizahlen
Frage
Mit der Formel von Binet lässt sich die
n-te Fibonacci-Zahl a
n wie folgt berechnen:
Bei der Herleitung wird vorausgesetzt, dass die Fibonacci-Folge eine geometrische Folge
ist. Dann ist q
n das n-te Folgeglied und somit gilt: q
n+2
- q
n+1 - q
n = 0 usw. Aber wieso ist 1, 1, 2, 3 ...
eine geometrische Folge?
Antwort
Die besagte Herleitung ist zwar populär, aber nicht korrekt. Die Fibonaccizahlen bilden keine geometrische Folge, weil die Quotienten aus benachbarten Folgegliedern verschieden sind.
Stattdessen kann man
die Fibonaccifolge um das Glied a
o
= 0 erweitern, dann gilt für alle n die Aussage
a
n+1 = a
n +
a
n-1. Zusammen mit der Gleichung a
n =
a
n +
0
· an-1
erhält man ein lineares Gleichungssystem. A sei die Koeffizientenmatrix, dann liefert
(an+1 an)t
=
An · (1 0)t
die Formel von Binet, wobei man A
n durch Diagonalisierung der Matrix A bestimmt. Hierfür sind Kenntnisse der Linearen Algebra erforderlich.
Diagonalisierung der Matrix A
Das o.g. lineare Gleichungssystem kann man wie folgt aufschreiben:
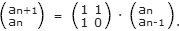
Die Matrix in der Mitte bezeichnen wir mit A und erhalten
Gleichung (1):
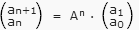
mit a
1 = 1, a
0 = 0. Um A
n bestimmen zu können, berechnen wir die Eigenwerte von A, wobei
T²-T-1 das charakteristische Polynom von A ist.
Die 2×2-Matrix A hat also zwei Eigenwerte
λ1 =
½+½·√5 ,
λ2 =
½-½·√5
und ist daher diagonalisierbar. Die zugehörigen Eigenvektoren
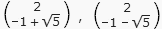
bilden zusammen eine invertierbare 2×2-Matrix S, und
S
-1·A
·S =: D
ist eine Diagonalmatrix, deren Diagonalelemente
die Eigenwerte λ
1 und λ
2 sind. Wir multiplizieren jetzt von links mit S und von rechts mit S
-1, daraus folgt
A = S
·D
·S
-1, also gilt:
A
n = S
·D
n·S
-1.
Hierbei ist D
n wieder eine Diagonalmatrix mit den
Diagonalelementen
(λ1)n und
(λ2)n.
Damit kann man
An·(1 0)t
berechnen -
Gleichung (1) liefert nun die Formel von Binet.




