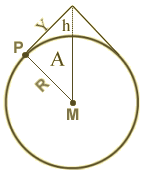
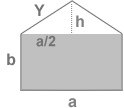
Eine populäre Denksportaufgabe lautet: Umspanne eine Kugel (etwa die Erde) straff mit einem Seil und verlängere es um einen Meter. Mehr oder minder erstaunt stellt man nun fest, dass das Seil überall rund 16 cm absteht, weil die Gleichung 2π·R + 1 = 2π·(R+x) die Lösung x = 1/2π hat. Dieser Abstand ist also unabhängig vom Radius R und somit von der Größe der Kugel. Folgende Variante der Aufgabe ist aber wirklich verblüffend:

So paradox es anmutet: Je größer die Kugel ist, umso höher lässt sich das Seil ziehen, wenn es einen Meter (oder auch nur Millimeter) länger als der Kugelumfang ist. Am Rechteck kann man das noch besser nachvollziehen:

Das Seil bzw. die Schnur habe jetzt also die Länge 2a+2b+1. Wegen |Y| - ½ = ½·a folgt aus dem Satz des Pythagoras: h = ½·√2a + 1.  Spannt man zum Beispiel eine Schnur um ein Rechteck der Seitenlänge a = 10 cm und gibt noch 1 cm Schnurlänge hinzu, so beträgt h rund 2,3 cm. Bei einer Seitenlänge von a = 100 cm ergeben sich für h bereits mehr als 7 cm - daher ist es so schwierig, große Pakete ganz straff zu schnüren. Die Schnur kann man natürlich nicht so weit hochziehen, wenn man sie an der kürzeren Paketseite fasst.