Der Inhalt eines Kegels passt genau dreimal in den Zylinder mit gleicher Höhe H und Radius R hinein. Folglich hat der Kegel das Volumen V = R²·π·H/3. Per Strahlensatz erhält man nun den Inhalt vom Kegelstumpf:

Bemerkung

Wir zeigen jetzt, dass ein Kreiskegel mit Radius R und Höhe H tatsächlich den Rauminhalt V = R²·π·H/3 hat. Wir füllen den Kegel mit n maximalen Zylindern der Höhe H/n auf und projizieren ihn in die x-y-Ebene.

Der kleinste Zylinder beginnt in der Kegelspitze (an der Stelle x = 0) und hat den Radius f(0) = 0. Daran grenzt der Zylinder mit Radius f(1·H/n). Der nächste Zylinder hat den Radius f(2·H/n). So fortfahrend enden wir beim Radius f((n-1)·H/n). Die Summe s(n) aller Zylinderinhalte beträgt:

Wir wählen hier die Bezeichnung s(n), weil diese Summe von der Zahl n abhängt. Unsere Zylinder werden nämlich mit steigender Anzahl n stets flacher, wodurch jede einzelne Lücke zwischen Kegelmantel und Zylinder schrumpft. Andererseits gibt es dann aber immer mehr Zwischenräume - daher stellt sich die Frage, ob die Anzahl oder die Winzigkeit der Lücken entscheidend ist:

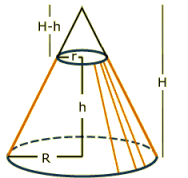
Jedenfalls ist s(n) niemals größer als das Kegelvolumen V, weil der Kegel stets alle n Zylinder enthält - folglich gilt: s(n) ≤ V. Die monoton steigende Folge der Zahlen s(n) ist also nach oben beschränkt und hat somit einen Grenzwert g, der offensichtlich mit R²·π·H/3 übereinstimmt. Wir können aber nicht ausschließen, dass g kleiner als V ist. Daher umfassen wir den Kegel mit einer Reihe von n Zylindern, die wiederum jeweils die Höhe H/n haben. Der kleinste Zylinder enthält die Kegelspitze und hat den Radius f(1·H/n). Der größte Zylinder, dessen Grundfläche jetzt identisch mit der des Kegels ist, hat also den Radius f(n·H/n) = R. Zusammen liefern die n Zylinder den Rauminhalt S(n):=

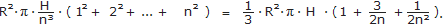
Weil der Kegel innerhalb der Zylinderreihe liegt, erhalten wir für alle n die Abschätzung: S(n) ≥ V. Ferner sieht man sofort, dass die Folge der S(n) gegen den Grenzwert G = R²·π·H/3 konvergiert. Damit ist g = G und wegen s(n) ≤ V ≤ S(n) gilt zudem: g ≤ V ≤ G. Daraus folgt schließlich die gesuchte Gleichung: V = R²·π·H/3.

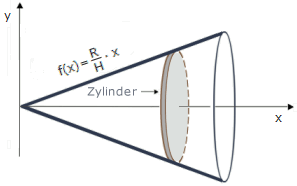
Diese Formel hätten wir auch kurzerhand durch das Integral:

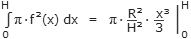
ermitteln können. Es führt aber kein Weg an unserer obigen Darstellung vorbei, wenn man die Inhaltsbestimmung per Integralrechnung wenigstens in den Grundzügen verstehen möchte.
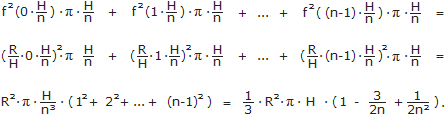